Sorting Algorithms

Here is how we formally define the sorting problem:

• Input: A sequence of $n$ numbers $(a1,a2,...,an)$
• Output: A permutation (reordering) $(a^{\prime }1,a^{\prime }2,...,a^{\prime }n)$ of the input sequence such that $a^{\prime }1<=a^{\prime }2<=...<=a^{\prime }n$

List of sorting algorithms:

1. Bubble: O(n^2) (also known as Simple Sort)
2. Insertion: O(n^2)
3. Selection: O(n^2)
4. Heap Sort: O(n log n)
5. Merge Sort: O(n log n)
6. Quick Sort: O(n log n)
7. Tree Sort: O(n log n)
8. Shell Sort: O(n^(3/2))
9. Count Sort: O(n)
10. Bucket/Bin Sort : O(n)
11. Radix Sort : O(n)

In the above list 1-8 are called Comparison based Sorts, And 9-11 are called Index based Sorts

Go to sorting overview

Criteria For Analysis

1. Number of Comparisons

2. Number of Swaps

3. Adaptive: Less time to sort an already sorted list. An adaptive sorting algorithm is one that takes advantage of the existing order of the input data to improve its efficiency. If an algorithm is adaptive, it performs fewer comparisons or swaps when dealing with partially sorted data

   • Efficient for data sets that are already substantially sorted

4. Stability: A sorting algorithm is stable if it maintains the relative order of equal elements in the sorted output as they were in the original input. In other words, if you have two equal elements A and B, and A appears before B in the input, a stable sorting algorithm will ensure that A still appears before B in the sorted output

   • Does not change the relative order of elements with equal keys

5. Extra Memory

Bubble Sort

It is also known as Simple Sort

Bubble Sort is a straightforward sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted

Steps:

1. Start with an unsorted list of elements

2. Compare the first element with the second element. If the first element is greater than the second element, swap them

3. Move to the next pair of elements (second and third) and repeat step 2

4. Continue this process for all adjacent pairs of elements in the list, comparing and swapping as necessary. After the first pass, the largest element will have "bubbled up" to the end of the list

5. Repeat steps 2-4 for a total of n-1 passes, where n is the number of elements in the list. On each pass, the largest unsorted element will move to the end of the list

6. After completing all passes, the list will be sorted

Pseudocode:

procedure bubbleSort(list)
    n = length(list)
    for i from 0 to n - 1
        for j from 0 to n - i - 1
            if list[j] > list[j + 1]
                swap(list[j], list[j + 1])
            end if
        end for
    end for
end procedure

Example:

Let's say you have an unsorted list: [5, 2, 9, 1, 5]

1. Pass 1: [2, 5, 1, 5, 9]
2. Pass 2: [2, 1, 5, 5, 9]
3. Pass 3: [1, 2, 5, 5, 9]

• After three passes, the list is sorted

For an array of size n at worst case:

• Number of Passes: n-1
• Max Number of Comparisons: (n * (n - 1)) / 2 --> O(n^2)
• Max Number of Swaps: (n * (n - 1)) / 2 --> O(n^2)

Time complexity:

• Best case: O(n)

• Worst case: O(n^2)

• By using a flag we can make it Adaptive

• For an Adaptive sort it will perform:

  • Comparisons: n-1
  • Swaps: 0
  • Performance: O(n)

• Bubble sort is Adaptive and Stable

It can be used to get some number of elements sorted, like finding the largest (or smallest if desc) number in 1 pass (the last element)

Implementations:

void Bubble_Sort(int A[], int n) {
  int i, j, temp = 0;
  int flag; // makes the sort Adaptive

  for (i = 0; i < n - 1; i++) {
    flag = 0;

    for (j = 0; j < n - i - 1; j++) {
      if (A[j] > A[j + 1]) {
        temp = A[j + 1];
        A[j + 1] = A[j];
        A[j] = temp;

        flag = 1;
      }
    }

    if (flag == 0)
      break;
  }
}

Insertion Sort

Insertion Sort is a simple sorting algorithm that builds the final sorted array one element at a time. It's based on the idea of iteratively inserting elements from the unsorted portion of the array into their correct positions within the sorted portion. This process continues until all elements are inserted and the entire array is sorted

Steps:

1. Initial State: The algorithm considers the first element as the initially sorted portion and the remaining elements as the unsorted portion

2. Iterative Insertion: For each element in the unsorted portion, the algorithm compares it to the elements in the sorted portion from right to left. It finds the correct position for the element within the sorted portion by shifting larger elements to the right

3. Insertion: Once the correct position is found, the element is inserted into its place within the sorted portion

4. Repeat: Steps 2 and 3 are repeated for all remaining elements in the unsorted portion until all elements have been inserted into the sorted portion

Pseudocode:

// A is 0 indexed array
for i = 1 to A.length:
    key = A[i]
    // Insert A[i] into the sorted sequence A[1..i-1]
    j = i - 1
    while j > 0 and A[j] > key:
        A[j + 1] = A[j]
        j = j - 1
    A[j + 1] = key

Examples:

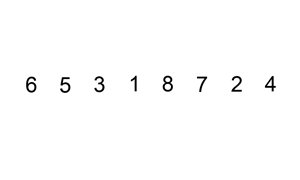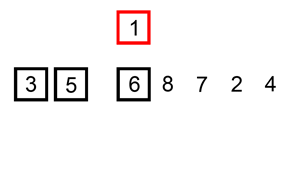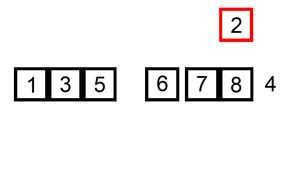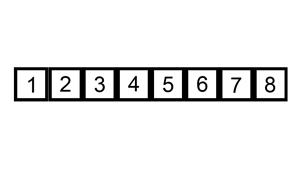
Let's say you have an unsorted list: [5, 2, 9, 1, 5]

1. Pass 1: [2, 5, 9, 1, 5]
2. Pass 2: [2, 5, 9, 1, 5]
3. Pass 3: [1, 2, 5, 9, 5]
4. Pass 4: [1, 2, 5, 5, 9]

Analysis:

1. Best Case Scenario:

   • Input: The input array is already sorted
   • Time Complexity: O(n)
   • Explanation: Each element is already in its correct position, so the algorithm only compares each element with the one before it and makes no swaps. The inner loop of the insertion sort algorithm will only execute once for each element. Therefore, it only performs n-1 comparisons, resulting in a linear time complexity
   • Max Number of Comparisons: n - 1 --> O(n)
   • Max Number of Swaps: 0 --> O(1)

2. Worst Case Scenario:

   • Input: The input array is sorted in reverse order
   • Time Complexity: O(n^2)
   • Explanation: In the worst case, each new element is smaller than all the elements already sorted. This requires the algorithm to compare the new element with all previous elements and shift them to the right, leading to a quadratic number of comparisons and swaps

   For an array of size n at worst case:

   • Number of Passes: n-1
   • Max Number of Comparisons: (n * (n - 1)) / 2 --> O(n^2)
   • Max Number of Swaps: (n * (n - 1)) / 2 --> O(n^2)

3. Average-Case Scenario:

   • Input: The input array is in a random order

   • Time Complexity: O(n^2)

   • Explanation:

     • On average, each element in the array is compared and potentially swapped with about half of the elements before it.
     • Specifically, for each element, about half of the previous elements are expected to be larger and need to be shifted to make room for the new element.
     • Since this happens for each of the n elements, the total number of comparisons and shifts sums to about $\frac{n^2}{4}$, which still results in a quadratic time complexity, O(n^2)

	Bubble Sort	Insertion Sort	Cases
Min Comparison	O(n)	O(n)	Already Sorted
Max Comparison	O(n^2)	O(n^2)	Sorted in Reverse
Min Swap	O(1)	O(1)	Already Sorted
Max Swap	O(n^2)	O(n^2)	Sorted in Reverse
Adaptive	Yes	Yes
Stable	Yes	Yes
Linked List	-	Yes
k Passes	Yes	No

Characteristics:

• Insertion Sort is particularly efficient when dealing with small arrays or partially sorted arrays, as the number of comparisons and shifts is relatively small in those cases

• More efficient in practice than most other simple quadratic algorithms such as selection sort or bubble sort

• It's an in-place sorting algorithm, meaning it doesn't require additional memory space proportional to the input size for sorting and with, at most, a constant number of them stored outside the array at any time

• Although the best-case time complexity of Insertion Sort is O(n) and the worst-case is O(n^2), the average-case also falls into O(n^2), reflecting that Insertion Sort generally performs similarly to its worst-case on typical, randomly ordered inputs

• This quadratic time complexity means that Insertion Sort is less efficient on average compared to more advanced sorting algorithms like Merge Sort or Quick Sort, especially as the input size grows

• Insertion is better for Linked List than Arrays

• By nature it is Adaptive

• It is Stable

• Online: can sort a list as it receives it

Loop Invariant

Loop invariant: At the start of each iteration of the for loop of lines 1–8, the subarray A[1..j-1] consists of the elements originally in A[1..j-1], but in sorted order

We use loop invariants to help us understand why an algorithm is correct. We must show three things about a loop invariant:

1. Initialization: It is true prior to the first iteration of the loop
2. Maintenance: If it is true before an iteration of the loop, it remains true before the next iteration
3. Termination: When the loop terminates, the invariant gives us a useful property that helps show that the algorithm is correct

When the first two properties hold, the loop invariant is true prior to every iteration of the loop

Selection Sort

Selection sort is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right

Steps:

1. Initial State: The algorithm starts with the entire array being unsorted and an empty sorted portion

2. Find the Minimum: In each iteration, the algorithm scans the unsorted portion of the array to find the minimum (or maximum) element

3. Swap: Once the minimum (or maximum) element is found, it's swapped with the leftmost element in the unsorted portion. This effectively moves the selected element to the end of the sorted portion

4. Expand Sorted Portion: After the swap, the sorted portion grows by one element, and the unsorted portion shrinks by one element

5. Repeat: Steps 2 to 4 are repeated until the entire array is sorted. The sorted portion gradually expands while the unsorted portion shrinks until there are no more elements left in the unsorted portion

6. Final State: At the end of the process, the array is fully sorted

Pseudocode:

function selectionSort(arr):
    n = length(arr)
    for i from 0 to n-2:  // The last element will be in the correct position after n-1 iterations
        minIndex = i
        for j from i+1 to n-1:
            if arr[j] < arr[minIndex]:
                minIndex = j
        if minIndex != i:
            swap(arr[i], arr[minIndex])

Example:

Let's say you have an unsorted list: [5, 2, 9, 1, 5]

1. Pass 1: Find the smallest, which is 1 and swap with left most 5: [1, 2, 9, 5, 5]
2. Pass 2: [1, 2, 9, 5, 5]
3. Pass 3: [1, 2, 5, 9, 5]
4. Pass 4: [1, 2, 5, 5, 9]
5. Pass 5: [1, 2, 5, 5, 9]

• Each element is compared in every operation, with number of operations same as the number of elements. With each operation an element is moved to the new array, so one less element to be compared in the next operation. On an average, (1/2)n elements are compared for each operation. Thus, the runtime is O(n x (1/2)n). But constants like (1/2) are ignored in Big O. So the runtime is written as O(n^2).

For an array of size n at worst case:

• Number of Passes: n-1

• Max Number of Comparisons: (n * (n - 1)) / 2 --> O(n^2)

• Max Number of Swaps: n-1 --> O(n)

• It is not Stable: does not guarantee stability. When selecting the minimum (or maximum) element to be placed in its correct position, Selection Sort doesn't consider the relative order of equal elements. As a result, if there are equal elements in the array, their order might change during the sorting process

• Is is not Adaptive: Its time complexity remains the same regardless of the input's initial order. It doesn't take advantage of any pre-existing order in the data. It always scans the entire unsorted portion of the array to find the minimum (or maximum) element, regardless of whether the array is partially sorted or not

• We get smallest (or largest if desc) number after just 1 pass (the first element)

Implementations:

def find_smallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

# Selection Sort
def selection_sort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = find_smallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr

Quick Sort

• It uses Divide & Conquer technique

• Partitioning procedure

• Not suited for sorted list or reverse sorted list

• Inductive proofs

• Randomized Quick Sort

• Selection Exchange Sort

• Partition Exchange Sort

Merge Sort

Merge Sort is a popular comparison-based sorting algorithm that follows the Divide-and-Conquer Algorithm strategy to efficiently sort an array or list of elements. It works by recursively dividing the array into smaller sub-arrays, sorting those sub-arrays, and then merging them back together to create a sorted final array

Steps:

1. Divide: The original array is recursively divided into smaller sub-arrays until each sub-array contains only one element or is empty

2. Conquer: The individual elements or small sub-arrays are already sorted by definition. This is the base case of the recursion

3. Merge: The sorted sub-arrays are then merged back together in a way that maintains their order. This merging process combines two sorted arrays into a single sorted array

In each step, it sorts a sub-array A[p:r] starting with the entire array A[1:n] and recursing down to smaller and smaller sub-arrays:

1. Divide the sub-array A[p:r] to be sorted into two adjacent sub-arrays, each of half the size. To do so, compute the midpoint q of A[p:r] (taking the average of p and r), and divide A[p:r] into sub-arrays A[p:q] and A[q+1:r]

2. Conquer by sorting each of the two sub-arrays A[p:q]and A[q+1:r] recursively using merge sort

3. Combine by merging the two sorted sub-arrays A[p:q] and A[q+1:r] back into A[p:r], producing the sorted answer

• The recursion "bottoms out" - it reaches the base case - when the sub-array A[p:r] to be sorted has just 1 element, that is, when p equals r

• The key operation of the merge sort algorithm occurs in the "combine" step, which merges two adjacent, sorted sub-arrays

• The merge operation is performed by the auxiliary procedure MERGE(A, p, q, r), where A is an array and p, q, and r are indices into the array such that p <= q < r

• The procedure assumes that the adjacent sub-arrays A[p:q] and A[q+1:r] were already recursively sorted

• It merges the two sorted sub-arrays to form a single sorted sub-array that replaces the current sub-array A[p:r]

Pseudocode:

Merge(A, p, q, r):
    nl = q - p + 1  // length of A[p:q]
    nr = r - q      // length of A[q+1:r]

    let L[0:nl - 1] and R[0:nr - 1] be new arrays

    for i = 0 to nl - 1:    // copy A[p:q] into L[0:nl - 1]
        L[i] = A[p + i]

    for j = 0 to nr - 1:    // copy A[q+1:r] into R[0:nl - 1]
        L[j] = A[q + j + 1]

    i = 0   // i indexes the smallest remaining element in L
    j = 0   // j indexes the smallest remaining element in R
    k = p   // k indexes the location in A to fill

    // As long as each of the arrays L and R contains an unmerged element,
    // copy the smallest unmerged element back into A[p:r]

    while i < nl and j < nr:
        if L[i] <= R[j]:
            A[k] = L[i]
            i = i + 1

        else:
            A[k] == R[j]
            j = j + 1
        k = k + 1

    // Having gone through on of L and R entirely, copy the
    // remainder of the other to the end of A[p:r]

    while i < nl:
        A[k] = L[i]
        i = i + 1
        k = k + 1
    while j < nr:
        A[k] = R[j]
        j = j + 1
        k = k + 1

// A is an array, p is starting index (0), r is the length of array - 1
Merge-Sort(A, p, r):
    if p >= r:                  // zero or one element?
        return

    q = floor((p + r)/2)        // midpoint of A[p:r]

    Merge-Sort(A, p, q)         // recursively sort A[p:q]
    Merge-Sort(A, q + 1, r)     // recursively sort A[q+1:r]

    // Merge A[p:q] and A[q+1:r] into A[p:r]
    Merge(A, p, q, r)

• Alternative, creating a new array:

function mergeSort(arr):
    if length(arr) <= 1:
        return arr

    mid = length(arr) / 2

    // Divide the array into left and right sub-arrays
    left = arr[0:mid]
    right = arr[mid:end]

    // Recursively sort the left and right sub-arrays
    left = mergeSort(left)
    right = mergeSort(right)

    // Merge the sorted sub-arrays
    sortedArray = merge(left, right)
    return sortedArray

function merge(left, right):
    result = []
    leftIndex = 0
    rightIndex = 0

    while leftIndex < length(left) and rightIndex < length(right):
        if left[leftIndex] <= right[rightIndex]:
            result.append(left[leftIndex])
            leftIndex++
        else:
            result.append(right[rightIndex])
            rightIndex++

    // Add remaining elements from both arrays
    while leftIndex < length(left):
        result.append(left[leftIndex])
        leftIndex++

    while rightIndex < length(right):
        result.append(right[rightIndex])
        rightIndex++

    return result

Analysis:

The running time of an algorithm on an input of size n by T(n), worst-case running time:

• Divide: The divide step just computes the middle of the sub-array, which takes constant time. Thus, D(n) = θ(1)

• Conquer: Recursively solving two sub-problems, each of size n/2, contributes 2T(n/2) to the running time (ignoring the floors and ceilings)

• Combine: Since the MERGE procedure on an n-element sub-array takes θ(n) time, we have C(n) = θ(n)

• Adding θ(n) to the 2T(n/2) term from the conquer step gives the recurrence for the worst-case running time T(n) of merge sort:

T(n) = 2T(n/2) + θ(n)

T(n) = {
    c1                  if n <= 1
    2T(n/2) + (c2 * n)  if n > 1
}

c1 > 0, represents the time required to solve a problem of size 1
c2 > 0, time per array element of the divide and combine steps

Using the Master Theorem, we can solve this recurrence relation to obtain the time complexity:

• a = 2: The number of sub-problems
• b = 2: The size of each sub-problem
• c = 1: The work done in combining the sub-problems

Since log_b(a) = log_2(2) = 1 and c = 1, the case of the Master Theorem that applies is:

T(n) = O(n^log_b(a) * log^k(n))
     = O(n^1 * log^0(n))
     = O(n log n)

1. Best Case Scenario:

   • Input: The input array is already sorted
   • Time Complexity: O(n log n)
   • Explanation: Merge sort still divides the array into smaller sub-arrays and merges them back together, but since the sub-arrays are already sorted, the merging process is very efficient

2. Worst Case Scenario:

   • Input: The input array is sorted in reverse order
   • Time Complexity: O(n log n)
   • Explanation: This results in the maximum number of comparisons and merges during the algorithm. However, the time complexity remains O(n log n) because the merging process is still efficient even in the worst case.

3. Average Case Scenario:

   • Input: The input array is in a random order
   • Time Complexity: O(n log n)
   • Explanation: On average, Merge Sort also requires O(n log n) time. The average case behaves similarly to the best and worst cases due to the algorithm's consistent approach of dividing and merging

Characteristics:

• Merge Sort is stable and consistent, and its performance does not degrade with input order

• Making it reliable and efficient sorting algorithm, particularly for large datasets

• The merging process is the key to Merge sort's efficiency, regardless of the input array's order

• It is Stable: During the merging step, when two elements are compared and inserted into the merged array, if they are equal, the element from the left sub-array is inserted before the element from the right sub-array. This maintains the relative order of equal elements, making Merge Sort a stable sorting algorithm

• It is Adaptive: Although its basic structure doesn't inherently take advantage of partially sorted data, its time complexity remains efficient even when dealing with partially sorted arrays. The reason is that Merge Sort always divides the array into smaller sub-arrays and eventually merges them. This merging process efficiently combines even small sorted sub-arrays into larger sorted sub-arrays. While not as inherently adaptive as algorithms like Insertion Sort, Merge Sort still performs well with partially sorted data due to its divide-and-conquer nature

Count Sort

• Index based sorting

Bucket/Bin Sort

Shell Sort

Uses Insertion Sort

Overview

Here's a comparison of the average-case time complexities of various sorting algorithms:

Algorithm	Space Complexity	Time Complexity (Worst)	Best	Avgerage	Adaptive	Stable
Bubble Sort	O(1)			O(n^2)	Yes	Yes
Selection Sort	O(1)			O(n^2)	No	No
Insertion Sort	O(1)			O(n^2)	Yes	Yes
Merge Sort	O(n)			O(n log n)	Yes	Yes
Quick Sort	O(log n)			O(n log n)	No	No (can be made)
Heap Sort	O(1)			O(n log n)	No	No
Counting Sort	O(k)			O(n + k) (k = range of input values)	No	Yes
Radix Sort	O(n + k)			O(nk) (k = number of digits in the maximum number)	No	Yes
Bucket Sort	O(n + k)		O(n) (uniform distribution)	O(n^2)	No	Yes

Space Complexity:

• All O(1) are In-place algorithm, hence no additional space is required
• Merge sort: Requires additional space for merging sub-arrays, not in-place
• Quick Sort: Recursive algorithm, requires additional space for the call stack
• Counting Sort: Requires additional space for counting array, where k is the range of input values
• Radix Sort: Requires additional space for intermediate arrays, where k is the number of digits in the maximum number
• Bucket Sort: Requires additional space for buckets and intermediate arrays, can be high for small ranges