Algorithms

Informally, an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform the input into the output.

An algorithm is said to be correct if, for every input instance, it halts with the correct output

Problem-solving vs Programming:

Problem-solving: Maths is required to solve problems. Maths does not have loops; it has Recursion. It's a lifetime of work
Programming: Learning the syntax of a language and implementing the solution in it

Analysing Algorithms

Analysing an algorithm has come to mean predicting the resources that the algorithm requires (mostly compute time and space)

Employ mathematical tools such as combinatorics, probability theory, algebraic dexterity, and the ability to identify the most significant terms in a formula

One way to analyse an algorithm is to run and collect metrics like memory usage, time to execute, CPU usage, etc. But there are several issues with this approach:

Running an algorithm on a computer provides timing data specific to that computer, input, implementation, compiler, libraries, and concurrent tasks
Timing results can vary even on the same computer with the same input
Single-timing runs offer limited insight into the algorithm's performance on different inputs, computers, or implementations

So, instead of relying on timing runs, analyse the algorithm by counting pseudocode line executions and evaluating their execution times. The analysis produces a precise formula for running time, which can be simplified using convenient notation to compare algorithms

Input size:

Running time depends on input size, with larger inputs generally taking more time to sort
The focus is on input size, the primary factor affecting running time, described as a function of input size
The appropriate measure of input size varies by problem, depending on factors like the number of items, bits (like multiplying 2 integers), or specific characteristics such as vertices and edges in a graph

Defining running time:

Running time is the number of instructions and data accesses executed, independent of any specific computer, based on the RAM model
Assume each line of pseudocode takes a constant amount of time, reflecting typical implementation on most computers

Example: Analysing Insertion Sort

The running time of an algorithm on an input of size n by T(n)

text

INSERTION-SORT(A, n)                cost  times
1 for i = 1 to n                    c1    n
2     key = A[i]                    c2    n - 1
3     j = i - 1                     c3    n - 1
4     while j > 0 and A[j] > key    c4    $\sum_{i=1}^{n} t_i$
5         A[j + 1] = A[j]           c5    $\sum_{i=1}^{n} (t_i - 1)$
6         j = j - 1                 c6    $\sum_{i=1}^{n} (t_i - 1)$
7     A[j + 1] = key                c7    n - 1

We have $t_{i} = 1$ for $i = 2, 3, . . ., n$ , and the best-case running time is given by:

\begin{aligned} T (n) & = c_{1} n + c_{2} (n - 1) + c_{3} (n - 1) + c_{4} (n - 1) + c_{7} (n - 1) \\ = (c_{1} + c_{2} + c_{3} + c_{4} + c_{7}) n - (c_{2} + c_{3} + c_{4} + c_{7}) \end{aligned}

We can express this running time as $a_{n} + b$ for constants $a$ and $b$ that depend on the statement costs $c_{k}$ (where $a = c_{1} + c_{2} + c_{4} + c_{5} + c_{8}$ and $b = c_{2} + c_{4} + c_{5} + c_{8}$ ). The running time is thus a linear function of $n$
In analysing Insertion Sort, we simplified by:
- Using constants ck to represent statement costs.
- Simplifying expressions further:
  - Best-case: $a n + b$
  - Worst-case: $a n^{2} + b n + c$
- Where $a$ , $b$ , and $c$ depend on $c_{k}$
This approach ignores both actual and abstract statement costs, providing a more generalized complexity analysis

Order of growth

It is the rate of growth, or order of growth, of the running time that really interests us

We consider only the leading term and ignore constant coefficients, as they're less significant for large inputs
Constant factors matter less than growth rate for large inputs

Example: For $n^{2} / 100 + 100 n + 17 m i c r o s e c o n d s$ , $n^{2} / 100$ dominates when $n > 10, 000$

Greek letter Θ‚ (theta) Θ-notation represents order of growth:

Insertion sort worst-case: Θ(n^2)
Insertion sort best-case: Θ(n)

Θ-notation informally means "roughly proportional when n is large"

Algorithms with lower order of growth in worst-case are generally considered more efficient
For sufficiently large inputs, a Θ(n^2) algorithm always outperforms a Θ(n^3) algorithm, regardless of hidden constants

Usually (but not always) we concentrate on finding only the worst-case running time, because:

Guarantee of Performance: The worst-case analysis provides an upper bound on the running time, ensuring that the algorithm will not exceed this time, no matter the input. This feature is especially important for real-time computing, in which operations must complete by a deadline
Relevance in Practice: For some algorithms, the worst case occurs fairly often. For example, in searching a database for a particular piece of information, the searching algorithm's worst case often occurs when the information is not present in the database. In some applications, searches for absent information may be frequent

RAM Model

The RAM (Random Access Machine) model is a theoretical framework that analyses algorithms by simplifying how a computer operates. Here are the main points:

Single Processor: The RAM model assumes a single processor that executes one instruction at a time, which is sequentially fetched from memory
Constant Time Operations: Basic operations like addition, subtraction, multiplication, division, comparison, and data access take constant time (O(1))
Memory Access: Memory is uniformly accessible, meaning any memory location can be accessed in constant time, regardless of its location
Word Size: The word size (the number of bits in a machine word) is assumed to be large enough to hold any data value or address used by the algorithm
No Parallelism: The model does not account for parallel processing; all operations are performed sequentially
Instruction Set: The model uses a basic set of instructions, similar to those in real computers, but abstracted to focus on algorithm efficiency rather than implementation details

This model helps provide a clear, consistent basis for analysing the time complexity of algorithms, independent of specific hardware or programming languages

Asymptotic Notation

The efficiency of an algorithm depends on the amount of time, storage and other resources required to execute the algorithm. The efficiency is measured with the help of asymptotic notations

The study of change in performance of the algorithm with the change in the order of the input size is defined as asymptotic analysis

Asymptotic notation can apply to functions that characterize some other aspect of algorithms (the amount of space they use, for example), or even to functions that have nothing whatsoever to do with algorithms.
Algorithm times are measured in terms of growth of an algorithm

"How many 2's do we multiply together to get 128?"

\log_{2} 128 = 7

Asymptotic Equivalence $\sim$ :

n^{2} \sim n^{2} + n

Because

lim_{n \to \infty} \frac{n^{2} + n}{n^{2}} = lim_{n \to \infty} 1 + \frac{1}{n} = 1

- $\sim$ is symmetric

Proof: Say $f \sim g$ . Now:

lim \frac{g}{f} = lim \frac{1}{\frac{f}{g}} = \frac{1}{lim \frac{f}{g}} = \frac{1}{1}

Transitivity of $\sim$ : Suppose $f \sim g$ and $g \sim h$ , prove $f \sim h$

1 = lim \frac{f}{g} = lim \frac{\frac{f}{h}}{\frac{g}{h}} = \frac{lim \frac{f}{h}}{lim \frac{g}{h}}

1 = \frac{lim \frac{f}{h}}{1}

Corollary: $\sim$ is an equivalence relation

Summary:

Func	Desc
$f \sim g$	$f$ & $g$ nearly equal
$f = o (g)$	$f$ much less than $g$
$f = O (g)$	$f$ roughly ≤ $g$
$f = Θ (g)$	$f$ roughly equal $g$

Big O (O-notation)

O-notation characterizes an upper bound on the asymptotic behaviour of a function

It says that a function grows no faster than a certain rate, based on the highest-order term

Definition: For a given function $g (n)$ , we denote by $O (g (n))$ (pronounced "big-oh of $g$ of $n$ " or sometimes just "oh of $g$ of $n$ ") the set of functions:

text

O(g(n)) = {
            f(n): there exist positive constants `c` and `n0` such that
                  0 ≤ f(n) ≤ cg(n) for all n ≥ n0
}

Example: $f (n) = 2 n^{2} + 3 n$ is $O (n^{2})$ because for $c = 3$ and $n_{0} = 3$ , $2 n^{2} + 3 n \leq 3 n^{2}$ for all $n \geq 3$

$f (n)$ grows no faster than $g (n)$ in the worst case

Big O is the most commonly used notation

Dominant term of the function is taken for consideration
Big-O notation represents the upper bound of the running time of an algorithm
It provides the worst-case scenario, representing the maximum amount of time an algorithm could take as the input size increases

Example: Function $7 n^{3} + 100 n^{2} - 20 n + 6$

Its highest-order term is $7 n^{3}$ , and so we say that this function's rate of growth is $n^{3}$
Because this function grows no faster than $n 3$ , we can write that it is $O (n^{3})$
This function is also $O (n^{4})$ . Why? Because the function grows more slowly than $n^{4}$ , we are correct in saying that it grows no faster
Hence, this function is also $O (n^{5})$ , $O (n^{6})$ , and so on
More generally, it is $O (n^{c})$ for any constant $c \geq 3$

Basically:

How code slows as data grows
Not the same as running time
Big trend over time

"Big O notation is a mathematical notation that describes the limiting behaviour of a function when the argument tends towards a particular value or infinity. It is a member of a family of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation."

Big Omega (Ω-notation)

Ω-notation characterizes a lower bound on the asymptotic behaviour of a function

It says that a function grows at least as fast as a certain rate, based as in O-notation - on the highest-order term
Because the highest-order term in the function $7 n^{3} + 100 n^{2} - 20 n + 6$ grows at least as fast as $n^{3}$ , this function is $Ω (n^{3})$ . This function is also $Ω (n^{2})$ and $Ω (n)$
More generally, it is $Ω (n^{c})$ for any constant $c \leq 3$
It represents the best-case scenario, showing the minimum amount of time an algorithm will take

Definition: For a given function $g (n)$ , we denote by $Ω (g (n))$ (pronounced "big-omega of $g$ of $n$ " or sometimes just "omega of $g$ of $n$ ") the set of functions:

text

Ω(g(n)) = {
            f(n): there exist positive constants `c` and `n0` such that
                  0 ≤ cg(n) ≤ f(n) for all n ≥ n0
}

Example: $f (n) = n^{2} / 2 - 2 n$ is $Ω (n^{2})$ because for $c = 1 / 4$ and $n_{0} = 8$ , $n^{2} / 4 \leq n^{2} / 2 - 2 n$ for all $n \geq 8$

$f (n)$ grows at least as fast as $g (n)$ in the best case

Theta (Θ-notation)

Θ-notation characterizes a tight bound on the asymptotic behaviour of a function

It says that a function grows precisely at a certain rate, based on the highest-order term
Characterizes the rate of growth of the function to within a constant factor from above and to within a constant factor from below. These two constant factors need not be equal
Since the function $7 n^{3} + 100 n^{2} - 20 n + 6$ is both $O (n^{3})$ and $Ω (n^{3})$ , it is also $Θ (n^{3})$

Definition: For a given function $g (n)$ , we denote by $Θ (g (n))$ (pronounced "theta of $g$ of $n$ ") the set of functions:

text

Θ(g(n)) = {
            f(n): there exist positive constants `c1`, `c2`, and `n0` such that
                  0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0
}

Theorem: For any two functions $f (n)$ and $g (n)$ , we have $f (n) = Θ (g (n))$ if and only if $f (n) = O (g (n))$ and $f (n) = Ω (g (n))$

Example: $f (n) = 3 n^{2} + 2 n - 1$ is $Θ (n^{2})$ because for $c 1 = 2$ , $c 2 = 4$ , and $n 0 = 2$ , $2 n^{2} \leq 3 n^{2} + 2 n - 1 \leq 4 n^{2}$ for all $n \geq 2$

Theta (Θ()) describes the exact bound of the complexity
Theta notation encloses the function from above and below
Since it represents the upper and the lower bound of the running time of an algorithm, it is used for analysing the average-case complexity of an algorithm

Other Notations

Little O (o-notation): For a given function $g (n)$ , we denote by $o (g (n))$ ("little-oh of $g$ of $n$ ") the set of functions:
text
```
o(g(n)) = {
            f(n): for any positive constant `c > 0`, there exists a constant
                  n0 > 0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0
}
```
Example: $f (n) = n i s o (n^{2})$ because for any $c > 0$ , we can choose $n_{0} = 1 / c$ , and then $n < c n^{2}$ for all $n > n_{0}$
- Little O describes the upper bound excluding the exact bound (i.e. denote an upper bound that is not asymptotically tight)
Little-omega (𝜔-notation): For a given function $g (n)$ , we denote by $𝜔 (g (n))$ ("little-omega of $g$ of $n$ ") the set of functions:
text
```
𝜔(g(n)) = {
            f(n): for any positive constant `c > 0`, there exists a constant
                  n0 > 0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0
}
```
Example: $f (n) = n^{2} i s 𝜔 (n)$ because for any $c > 0$ , we can choose $n_{0} = c + 1$ , and then $c n < n^{2}$ for all $n > n_{0}$

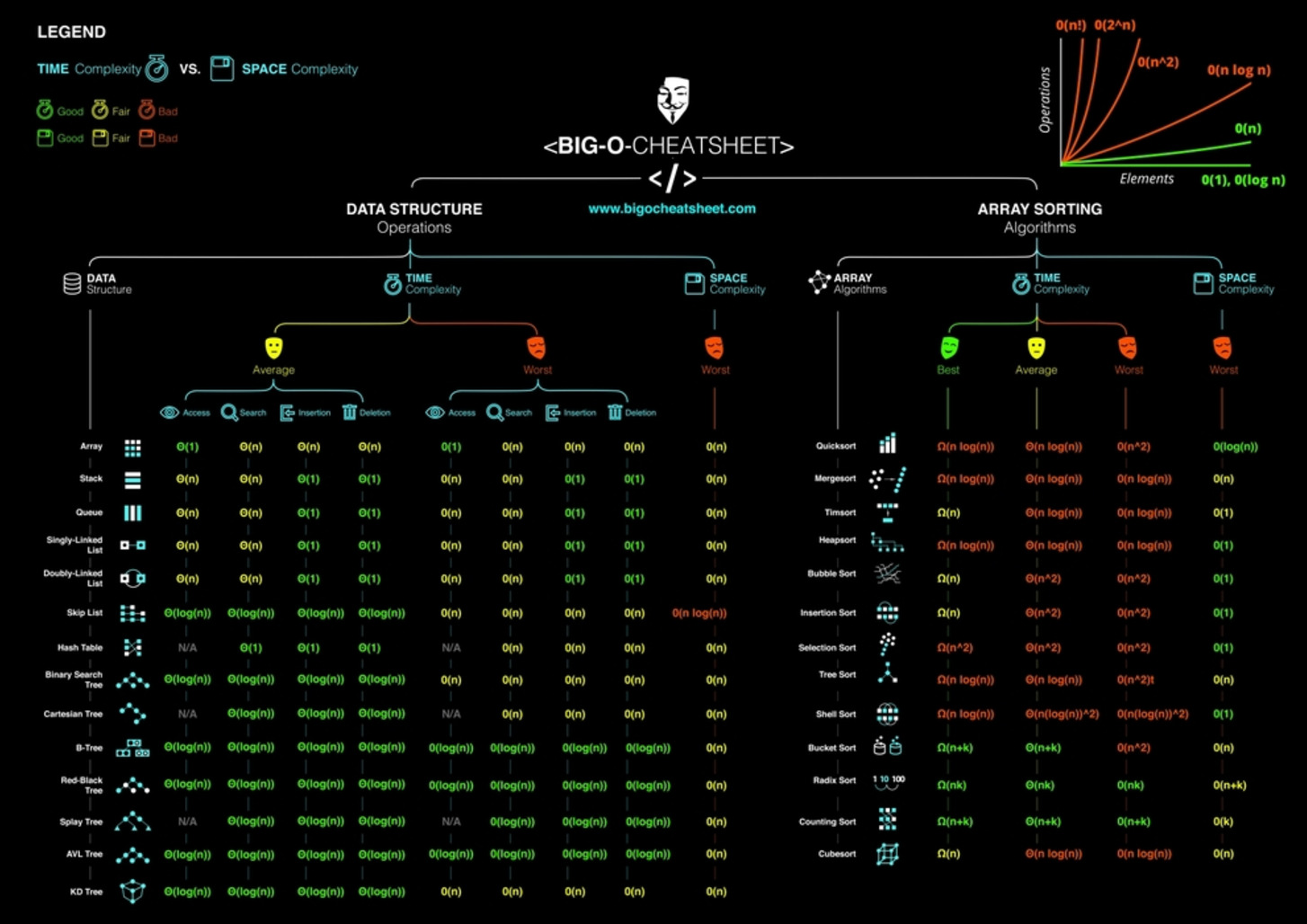
Time and Space Complexity

There are often many approaches to solving a problem. How do we choose between them? At the heart of computer program design are two (sometimes conflicting) goals:

To design an algorithm that is easy to understand, code, and debug
To design an algorithm that makes efficient use of the computer's resources

The method for evaluating the efficiency of an algorithm or computer program is called asymptotic analysis

A method for estimating the efficiency of an algorithm or computer program by identifying its growth rate. Asymptotic analysis also gives a way to define the inherent difficulty of a problem. We frequently use the term algorithm analysis to mean the same thing
Asymptotic analysis also gives a way to define the inherent difficulty of a problem

Order of the polynomial equation or Big O: How time scales with respect to some input variables

Usually n is used to denote the variable (any letter can be used)

Rules:

Different steps get added: O(a) and O(b) will be added to O(a+b)
Drop constants: If the complexity is 2n, the constant 2 is dropped and Big O is represented as O(n)
Different inputs should use different variables. So, instead of using n for two different arrays use a and b. So, Big O is O(a * b) not O(n^2)
Drop non-dominate terms: If a function has two complexities such as O(n) and O(n^2). Drop O(n) and just use O(n^2)

O(n):

// one for loop
for (int i=0; i<n; i++) {
    /* Code */
    }

O(n^2):

// one for loop
for (int i=0; i<n; i++) {
    for (int i=0; i<n; i++) {
    /* Code */
    }
}

Time functions

Terms:

complexity
- Complexity is different for small numbers than large numbers
time complexity
algorithmic complexity
asymptotic complexity
Amortization:
- Long-term averaging
- Operations can take different times
Worst case:
- Typical case vs worst case

Terminology:

O(...n...)
n: how much data
O: "Order of"
Not a function! (It's just a notation)

Big-O Complexity:

Big-O Complexity Chart

O(1): Constant time (size of data dose not matter)

Constant time beats linear if data is sufficiently big

python

# Array
arr = [1, 2, 3]
arr.append(4)    # push to end
arr.pop()        # pop from end
arr[0]           # lookup
arr[1]
arr[2]

# HashMap/Set
hashMap = {}
hashMap["key"] = 10     # insert
print("key" in hashMap) # lookup
print(hashMap["key"])   # lookup
hashMap.pop("key")      # remove

O(n): Linear time

Time grows proportionally to data

python

arr = [1, 2, 3]
sum(arr)           # sum of array
for n in arr:      # looping
   print(n)

arr.insert(1, 100) # insert
arr.remove(100)    # remove
print(100 in arr)  # search

import heapq
heapq.heapify(arr) # build heap

# sometimes even nested loops can be O(n)
# (e.g. monotonic stack or sliding window)

O(n^2): Quadratic time

python

# Traverse a square grid
arr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for i in range(len(arr)):
   for j in range(len(arr[i])):
      print(arr[i][j])


# Get every pair of elements in array
arr = [1, 2, 3]
for i in range(len(arr)):
   for j in range(i + 1, len(arr)):
      print(arr[i], arr[j])

# Insertion sort (insert in middle n times -> n^2)

O(n*m):

python

# Get every pair of elements from two arrays
arr1, arr2 = [1, 2, 3], [4, 5]
for i in range(len(arr1)):
   for j in range(len(arr2)):
      print(arr1[i], arr2[j])

# Traverse rectangle grid
arr = [[1, 2, 3], [4, 5, 6]]
for i in range(len(arr)):
   for j in range(len(arr[i])):
      print(arr[i][j])

O(n^3): and so on

python

# Get every triplet of elements in array
arr = [1, 2, 3]
for i in range(len(arr)):
   for j in range(i + 1, len(arr)):
      for k in range(j + 1, len(arr)):
            print(arr[i], arr[j], arr[k])

O(log n):

python

# Binary search
arr = [1, 2, 3, 4, 5]
target = 6
l, r = 0, len(arr) - 1
while l <= r:
   m = (l + r) // 2
   if target < arr[m]:
      r = m - 1
   elif target > arr[m]:
      l = m + 1
   else:
      print(m)
      break

# Binary Search on BST
def search(root, target):
   if not root:
      return False
   if target < root.val:
      return search(root.left, target)
   elif target > root.val:
      return search(root.right, target)
   else:
      return True

# Heap Push and Pop
import heapq
minHeap = []
heapq.heappush(minHeap, 5)
heapq.heappop(minHeap)

O(n log n):

python

# Heap Sort
import heapq
arr = [1, 2, 3, 4, 5]
heapq.heapify(arr)     # O(n)
while arr:
   heapq.heappop(arr) # O(log n)

# Merge Sort (and most built-in sorting functions)

O(2^n):

python

# Recursion, tree height n, two branches
def recursion(i, arr):
   if i == len(arr):
      return 0
   branch1 = recursion(i + 1, arr)
   branch2 = recursion(i + 2, arr)

O(c^n):

python

# c branches, where c is sometimes n.
def recursion(i, arr, c):
   if i == len(arr):
      return 0

   for j in range(i, i + c):
      branch = recursion(j + 1, arr)

O(sqrt(n)):

python

# Get all factors of n
import math
n = 12
factors = set()
for i in range(1, int(math.sqrt(n)) + 1):
   if n % i == 0:
      factors.add(i)
      factors.add(n // i)

O(n!):
- Permutations
- Travelling Salesman Problem

Big-O Cheat Sheet Poster

Static and Global variables:

Call Stack

A call stack is a stack data structure that stores information about the active subroutines of a computer program.

The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out).

Algorithm Design

Master Theorem

Divide-and-Conquer Algorithm

Divide and conquer algorithm is a strategy of solving a large problem by:

Breaking the problem into smaller sub-problems
Solving the sub-problems, and
Combining them to get the desired output

A problem is recursively broken down into smaller sub-problems of the same type until they become simple enough to solve directly. The solutions to the sub-problems are then combined to give a solution to the original problem

Steps:

Divide the problem into one or more sub-problems that are smaller instances of the same problem
Conquer the sub-problems by solving them recursively
Combine the sub-problem solutions to form a solution to the original problem

Based on multi-branched Recursion

Example: Analysing Merge Sort

It's applications:

Binary Search
Quick Sort
Finding the GCD is an use case of D&C.
Check Euclid's algorithm for GCD.
Strassen's Matrix multiplication
Karatsuba Algorithm

P vs NP Problem

NP-Complete Problems

NP-Complete problems are a class of computational problems in computer science and mathematics that are considered to be among the hardest problems to solve efficiently

A problem is NP-Complete if it's in NP (Non-deterministic Polynomial time) and all other NP problems can be reduced to it in polynomial time

Key characteristics:

No known polynomial-time algorithm to solve them
Verifying a solution is relatively quick (polynomial time)
No one knows whether or not efficient algorithms exist for NP-complete problems
If an efficient algorithm exists for any one of them, then efficient algorithms exist for all of them
Several NP-complete problems are similar, but not identical, to problems for which we do know of efficient algorithms

Examples:

The Travelling Salesperson problem
Performance: O(n!)
Implementation
Boolean Satisfiability Problem (SAT)
Graph Colouring Problem
Subset Sum Problem

Famous Algorithms

Dynamic programming
Greedy algorithm
- Dijkstra's Shortest Path algorithm
Backtracking
Sliding window
Monotonic stack

References

Grokking Algorithms: An illustrated guide for programmers and other curious people, by Adiya Y. Bhargava
Introduction to Algorithms, 4th edition, by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein

Algorithms ​

Analysing Algorithms ​

Order of growth ​

RAM Model ​

Asymptotic Notation ​

Big O (O-notation) ​

Big Omega (Ω-notation) ​

Theta (Θ-notation) ​

Other Notations ​

Time and Space Complexity ​

Call Stack ​

Algorithm Design ​

Divide-and-Conquer Algorithm ​

P vs NP Problem ​

NP-Complete Problems ​

Famous Algorithms ​

References ​

Algorithms

Analysing Algorithms

Order of growth

RAM Model

Asymptotic Notation

Big O (O-notation)

Big Omega (Ω-notation)

Theta (Θ-notation)

Other Notations

Time and Space Complexity

Call Stack

Algorithm Design

Divide-and-Conquer Algorithm

P vs NP Problem

NP-Complete Problems

Famous Algorithms

References